Lep pozdrav!
Zanima me kako se funkcijo f(x)=-xIxI "prevede" v enostavnejšo obliko. (Če je sploh možno.)
Matematika
Re: Matematika
A ni to dovolj kompaktno? Ce bi se rad znebil absolutne vrednosti, kaj vec kot \(|x|=\sqrt{x^2}\) ne mores narest. Lahko pa jo poves po kosih:
\(f(x)=\begin{cases}
x^2 & x<0\\
-x^2 & x\geq 0
\end{cases}\)
Ali pa s predznakom:
\(f(x)=-(\mathrm{sgn\,}{x}) x^2\)
\(f(x)=\begin{cases}
x^2 & x<0\\
-x^2 & x\geq 0
\end{cases}\)
Ali pa s predznakom:
\(f(x)=-(\mathrm{sgn\,}{x}) x^2\)
Re: Matematika
Končujem gimnazijo, tako da je recimo ta sgn preveč zame. Ampak ok. Graf mi še uspe narisat tako da ustavim par točk... Potem pa je treba funkcijo integrirat. V rešitvah piše: \(\int_{-1}^{0}(-x-x^2)dx\) Iz tega bi jaz sklepal da velja: f(x)=-xIxI <=> f(x)=x^2 ..ampak ni tako (ker je potem graf drugačen). Če mi lahko kdo razsvetli problem. =P
Naloga:
Rešitve:
Naloga:
Rešitve:
Zadnjič spremenil Rorschach, dne 3.6.2009 15:22, skupaj popravljeno 1 krat.
Re: Matematika
sgn(x) vrne 1, če je x pozitiven, ali pa -1, če je x negativen (skratka sgn ti pove predznak x).
Aniviller je dobro napisal: za x> je tvoja funkcija enaka x^2, za x<0 pa -x^2. ker pa integriraš pri negativnih x (od -1 do 0), delaš kot da bi imel -x^2. če bi imel recimo meje od -2 do 3, bi od -2 do 0 upošteval f(x)=-x^2, od 0 do 3 pa f(x)=x^2.
Aniviller je dobro napisal: za x> je tvoja funkcija enaka x^2, za x<0 pa -x^2. ker pa integriraš pri negativnih x (od -1 do 0), delaš kot da bi imel -x^2. če bi imel recimo meje od -2 do 3, bi od -2 do 0 upošteval f(x)=-x^2, od 0 do 3 pa f(x)=x^2.
Re: Matematika
Ok.. torej postopek bi bil:
\(f(x)=-x|x|=-x\sqrt{x^2}=\begin{cases}
-x(-x)=x^2 & x<0\\
-x(x)=-x^2 & x\geq 0
\end{cases}\)
Hvala, bom še kaj vprašal...
\(f(x)=-x|x|=-x\sqrt{x^2}=\begin{cases}
-x(-x)=x^2 & x<0\\
-x(x)=-x^2 & x\geq 0
\end{cases}\)
Hvala, bom še kaj vprašal...
Re: Matematika
tko ja. jaz sem rpej pisal za f(x)= |x| x. predznaka nisem gledu, saj samo obrne stvar.
Re: Matematika
ja sem vseeno razumel 
c)
1.odvajam enačbo elipse \(y'=\left ( \frac{2-x}{4(y+1)} \right )\)
2.koeficient premice je \(\frac{\sqrt{3}}{2}\)
3.izenačim in dobim \(x=-2\sqrt{3}(y+1)+2\)
kaj zdaj?
c)
1.odvajam enačbo elipse \(y'=\left ( \frac{2-x}{4(y+1)} \right )\)
2.koeficient premice je \(\frac{\sqrt{3}}{2}\)
3.izenačim in dobim \(x=-2\sqrt{3}(y+1)+2\)
kaj zdaj?
Re: Matematika
ker sta točki na elipsi, velja tudi:
\((x-2)^2+4(y+1)^2=4\)
zdaj maš pa dve enačbi z dvema neznankama in lohk zračunaš tvoji dve točki (verjetno se splača tvoj x vstavt v enačbo elipse).
\((x-2)^2+4(y+1)^2=4\)
zdaj maš pa dve enačbi z dvema neznankama in lohk zračunaš tvoji dve točki (verjetno se splača tvoj x vstavt v enačbo elipse).
Re: Matematika
Aha...v bistvu moram vstavit v enačbo od elipse (ker premica gre mimo).
Kombinatorika:
Naloga c)
js rešim (po definiciji za permutacije s ponavljanjem):
6!/(3!×2!×1)+6!/(2!×3!×1)+6!/(1×4!×1)= (šestmestno število; 3 dvojke, 2 trojke, 1 enka)+(šestmestno število; 2dvojke, 3 trojke, 1 enka)+(šestmestno število; 1 dvojka, 3 trojke, 1 enka)
Kaj delam narobe?
------------
Permutacije s ponavljanjem so permutacije elementov, ki niso vsi med sabo različni. Pri tem lahko nastopa celo več skupin med sabo enakih elementov. Recimo, da je v prvi taki skupini k1 enakih elementov, v drugi k2 enakih elementov, ..., v m-ti pa km enakih elementov. Potem število permutacij s ponavljanjem izračunamo po formuli:
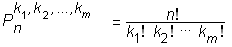
Kombinatorika:
Naloga c)
js rešim (po definiciji za permutacije s ponavljanjem):
6!/(3!×2!×1)+6!/(2!×3!×1)+6!/(1×4!×1)= (šestmestno število; 3 dvojke, 2 trojke, 1 enka)+(šestmestno število; 2dvojke, 3 trojke, 1 enka)+(šestmestno število; 1 dvojka, 3 trojke, 1 enka)
Kaj delam narobe?
------------
Permutacije s ponavljanjem so permutacije elementov, ki niso vsi med sabo različni. Pri tem lahko nastopa celo več skupin med sabo enakih elementov. Recimo, da je v prvi taki skupini k1 enakih elementov, v drugi k2 enakih elementov, ..., v m-ti pa km enakih elementov. Potem število permutacij s ponavljanjem izračunamo po formuli:
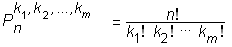
Re: Matematika
Jaz bi razmišlal tako: ker se enka pojavi natančno enkrat, jo postavimo na eno izmed šestih mest, zračunamo vse možnosti za to pozicijo in pomnožimo s 6. pri dani poziciji enke pa so za nas neustrezne tiste rešitve, ki so brez dvojke (to je samo ena), ki imajo eno dvojko (ki jo razporedimo na 5 mest) ali dve dvojki (2 dvojki in 3 trojke => 5!/(3!*2!). vseh možnosti pa je 2^5 (ker na pet mest lahko postavimo ali 3 ali 2.
torej lahko sestavimo \(6 (2^5 - (1 + 5 + 10)) = 96\).
torej lahko sestavimo \(6 (2^5 - (1 + 5 + 10)) = 96\).
Re: Matematika
Aha, če rešim na tvoj način:
6!/(3!×2!×1!)+6!/(4!×2!×1!)+6!/(5!×0!×1!) = 96
vsa so šestmestna št.;
prvi člen: 3 dvojke, 2 trojki, 1 enka
drugi člen: 4 dvojke, 1 trojka, 1 enka
tretji člen: 5 dvojk, 0 trojk, 1 enka
lp
6!/(3!×2!×1!)+6!/(4!×2!×1!)+6!/(5!×0!×1!) = 96
vsa so šestmestna št.;
prvi člen: 3 dvojke, 2 trojki, 1 enka
drugi člen: 4 dvojke, 1 trojka, 1 enka
tretji člen: 5 dvojk, 0 trojk, 1 enka
lp
Re: Matematika
ajaa kreten....zgleda da mam težave z razumevanjem vsaj =P
sm mislu lih obratno ("...največ trikrat")
ok zdej bo
sm mislu lih obratno ("...največ trikrat")
ok zdej bo
Re: Matematika
Kompleksna števila:
b)
-24+4+2ai+b=0
naprej pa ne znam...vem da bi mogu dobit nek sistem enačb...ampak kako?
b)
-24+4+2ai+b=0
naprej pa ne znam...vem da bi mogu dobit nek sistem enačb...ampak kako?
Re: Matematika
Osnovni izrek algebre pravi, da ničle polinoma nastopajo v konjugiranih parih, kar pomeni, da s tem, ko imaš ničlo 2i, imaš avtomatsko še drugo ničlo (-2i).
Enkrat si že naredil Hornerjev algoritem (za 2i), naredi ga še za -2i. Zadnji člen, ki ga dobiš enači z 0. In tako dobiš 2 enačbi z dvema neznankama, če ne boš znal rešt, povej.
Enkrat si že naredil Hornerjev algoritem (za 2i), naredi ga še za -2i. Zadnji člen, ki ga dobiš enači z 0. In tako dobiš 2 enačbi z dvema neznankama, če ne boš znal rešt, povej.
Re: Matematika
Kar se pa tiče c primera:
Dokaz s popolno indukcijo poteka v dveh korakih:
1.) dokažemo, da velja za majhne \(n\), npr za \(n=1\)
\((1+i)^{4}=-4\)
\((1+2i-1)^{2}=-4\)
\(-4=-4\)
2.) Predpostavimo, da velja za \(n\) (torej \((1+i)^{4n}=(-4)^{n}\) je sedaj res), dokažemo da velja za \(n+1\):
\((1+i)^{4(n+1)}=(-4)^{n+1}\)
\((1+i)^{4n}(1+i)^{4}=(-4)^{n}(-4)\)
Dobimo \((1+i)^{4n}=(-4)^{n}\) , to pa smo predpostavili, da je res. torej je dokaz končan.
2. koraku pravimo indukcijski korak. z njim pokažemo, da to velja za vsa naravna števila in sicer, da če velja za neko naravno število n, velja tudi za njegovega naslednjika n+1. In ker velja sedaj za naravno število n+1, velja tudi za njegovega naslednjika n+2, enako za n+3, n+4 itd..... s tem bi lahko šli v neskončnost.
V resnici je pa dovolj pokazati, da če velja za n velja za n+1 in lahko sklepamo da velja za vsa naravna števila. (zato indukcija - induktivno sklepanje)
Dokaz s popolno indukcijo poteka v dveh korakih:
1.) dokažemo, da velja za majhne \(n\), npr za \(n=1\)
\((1+i)^{4}=-4\)
\((1+2i-1)^{2}=-4\)
\(-4=-4\)
2.) Predpostavimo, da velja za \(n\) (torej \((1+i)^{4n}=(-4)^{n}\) je sedaj res), dokažemo da velja za \(n+1\):
\((1+i)^{4(n+1)}=(-4)^{n+1}\)
\((1+i)^{4n}(1+i)^{4}=(-4)^{n}(-4)\)
Dobimo \((1+i)^{4n}=(-4)^{n}\) , to pa smo predpostavili, da je res. torej je dokaz končan.
2. koraku pravimo indukcijski korak. z njim pokažemo, da to velja za vsa naravna števila in sicer, da če velja za neko naravno število n, velja tudi za njegovega naslednjika n+1. In ker velja sedaj za naravno število n+1, velja tudi za njegovega naslednjika n+2, enako za n+3, n+4 itd..... s tem bi lahko šli v neskončnost.
V resnici je pa dovolj pokazati, da če velja za n velja za n+1 in lahko sklepamo da velja za vsa naravna števila. (zato indukcija - induktivno sklepanje)