Kvarkadabra forum

Parameter \(\tau\) mora biti poljuben, ne pa izbran ad hoc.

Ne, rekel sem ti že, da je križna korelacija funkcija \(\tau\), ne pa število.

Poljuben? To pomeni če izberem tau = 100 ali pa 1, bo v redu?

To je malo nenavadno, saj vem kaj je tau. To je časovni zamik med signaloma pri katerem se istoležni elementi množijo in seštejejo v primeru diskretne oblike.

Ma, ne, \(\tau\) pustiš kot parameter, ki se seveda pri integriranju obnaša kot konstanta, zato je rezultat integriranja, t.j. križna korelacija, funkcija tega parametra.

Torej dobimo funkcijo, vendar ta funkcija nič ne pove o podobnosti.

DirectX11 napisal/-a: ↑

8.2.2017 17:33

Torej dobimo funkcijo, vendar ta funkcija nič ne pove o podobnosti.

Seveda pove, tam, kjer ima ekstrem(e), je največja podobnost, tam, kjer je ima ničle, ni podobnosti.

Kar pomeni, da sta signala podobna samo v nekaterih točkah.

Torej moram rešiti enačbo \(f(x) = 0\). In če ne najdem ničel potem sta si podobna.

Ah, ne, križna korelacija govori o podobnosti signalov, ki so poljubno zamaknjeni (zato pa parameter \(\tau\)). Recimo za banalen primer \(u_1(t)=\sin(t)\) in \(u_2(t)=\cos(t)\) je križna korelacija:

\(\displaystyle r_{u_1u_2}(\tau)=\int_0^{2\pi}\sin(t)\cos(t-\tau)dt=\pi\sin(\tau)\).

Ta funkcija ima (na intervalu \([-\pi,\pi]\)) ekstrema pri \(\tau=\pm\frac{\pi}{2}\) in ničlo pri \(\tau=0\).

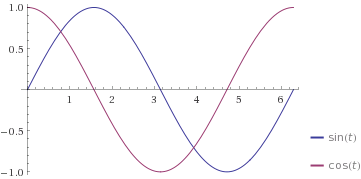
Iz tega je moč sklepati, da si sinus in kosinus nista podobna, če nista zamaknjena (\(\tau=0\)), t.j. \(\sin(t)\) in \(\cos(t)\):
in da sta si najbolj podobna, če je zamik bodisi \(\tau=\frac{\pi}{2}\), t.j. \(\sin(t)\) in \(\cos(t-\frac{\pi}{2})=\sin(t)\):
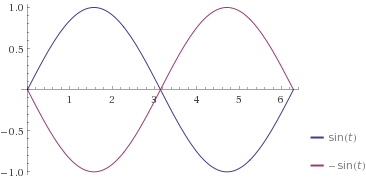
bodisi \(\tau=-\frac{\pi}{2}\), t.j. \(\sin(t)\) in \(\cos(t+\frac{\pi}{2})=-\sin(t)\):

Hvala za ta odličen primer. Danes sem poskusil na roke rešiti ta tvoj primer:

\(\int_0^{2\pi}\sin(t)\cos(t-\tau)dt=\)

Po uporabi trigonometrične identite:
\(\frac{1}{2} \int_0^{2\pi} \sin(2t - \tau) + \sin(\tau)dt=\)

\(\frac{1}{2} \int_0^{2\pi} \sin(2t - \tau)dt +\frac{1}{2} \int_0^{2\pi} \sin(\tau)dt=\)

Naredimo substitucijo v levem integralu: \(u = 2t - \tau\) torej, \(du = 2 dx \).

\(\frac{1}{4} \int_0^{2\pi} \sin(u)du +\frac{1}{2} \int_0^{2\pi} \sin(\tau)dt=\)

Nato nazaj vstavimo \(u\) ter meje \(0\) in \(2\pi\).

\(-\frac{1}{4} \cos(4\pi - \tau) + \frac{1}{4} \cos(-\tau) +\frac{1}{2} \int_0^{2\pi} \sin(\tau)dt=\)

Ali sem do te točke pravilno rešil? Rekel si da mora \(\tau\) ostati znotraj funkcij. Ampak ne vem kako postopati sedaj, saj imam sedaj funkcije samo s \(\tau\).

Saj sem ti že povedal, \(\tau\) se jemlje kot katerokoli drugo konstanto in zato se lahko \(\sin(\tau)\) izpostavi pred integral:

\(\displaystyle\frac{1}{2}\int_0^{2\pi}\sin(\tau)dt=\frac{1}{2}\sin(\tau)\int_0^{2\pi}dt\).

Integral je seveda enak \(2\pi\) in tako je izraz enak \(\pi\sin(\tau)\).

Ta vsota:

\(-\frac{1}{4}\cos(4\pi-\tau)+\frac{1}{4}\cos(-\tau)\)

pa je enaka 0, če veš, da je kosinus perodična funkcija s periodo \(2\pi\), t.j. \(\cos(x)=\cos(x+2k\pi);k\in\mathbb{Z}\).

P.S. S subsitucijo \(u=2t-\tau\Rightarrow du=2dt\), se v določenem integralu spremenijo tudi meje; če je \(t\) v mejah od \(0\) do \(2\pi\), mora biti \(u\) v mejah od \(-\tau\) do \(4\pi-\tau\)

\(\displaystyle\frac{1}{4} \int_{-\tau}^{4\pi-\tau}\sin(u)du\).

Recimo da imamo vezje iz uporov, katerih vrednosti so realna in imaginarna števila. Če sta taka upora vezana serijsko, ali se potem seštevajo tako kot je to ponavadi pri kompleksnih številih? Kaj pa če imamo napetostni vir podan tako: \(3e^{j45°}\), pri tem pa upor npr. \(3+10j\). Če hočemo izračunati tok bi morali vir deliti z vrednostjo upora. Vendar mi moj kalkulator to ne izračuna. Sem pa po Eulerjevi formuli pretvoril v sinusni signal, ter nato delil. Je to pravilno?

Hvala.

Kakor razumem, ko pretvorimo z Eulerjevo formulo za nek napetostni vir ne upoštevamo imaginarni del sinusa ampak samo realni kosinus. Saj to je mogoče logično saj vsi viri oddajajo napetost in tok brez časovnega zamika. Samo še vedno pa ne vem zakaj potem takšen zapis. Kaj dosežemo da napišemo kazalec napetosti, če imamo potem še velik dela s pretvorbo ter računanjem?

To je pa ja jasno: zapis v eksponentni obliki omogoča, da se operacije množenja in deljenja pretvori v operacije seštevanja in odštevanja.

Torej želiš povedati da tudi upore zapišem v eksponentni obliki. Zato da se potem eksponenta seštejeta?

Aja pa zmotil sem se glede zapisa uporov, upori imajo vedno samo realni del recimo 5 \(\Omega\). Saj ne ustvarijo časovnega zamika med napetostjo in tokom.

Ah, poglej si, no, še enkrat link: Če sta napetost in tok izražena v eksponentni obliki, je impedanca izražena kot eksponentna funkcija fazne razlike.