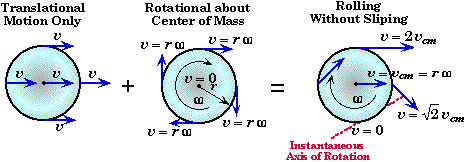Narobe so velikosti (dolžine) vektorjev hitrosti:
- vektor hitrosti na obodu na vrhu mora imeti dvakratno dolžino vektorja hitrosti v središču S (na sliki je daljši);
- vektorji hitrosti na obodu na istih višinah glede na točko stika s podlago P morajo imeti enako dolžino (na sliki so različnih dolžin).
Pravilna slika je:
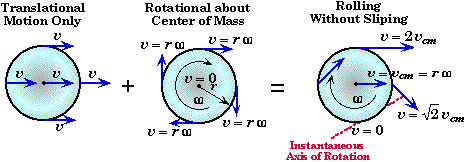
Iz tega je razvidno, da so hitrosti vektorska vsota hitrosti translacije in rotacije. Na obodu na vrhu je tako hitrost:
\(\vec{v}=\vec{v}_T+\vec{v}_R=(v_s,0)+(v_s,0)=(2v_s,0)\Rightarrow v=\sqrt{(2v_s)^2+0^2}=2v_s\)
Na obodu na levi strani na višini središča:
\(\vec{v}=\vec{v}_T+\vec{v}_R=(v_s,0)+(0,v_s)=(v_s,v_s)\Rightarrow v=\sqrt{v_s^2+v_s^2}=v_s\sqrt{2}\)
in na obodu na desni strani na višini središča:
\(\vec{v}=\vec{v}_T+\vec{v}_R=(v_s,0)+(0,-v_s)=(v_s,-v_s)\Rightarrow v=\sqrt{v_s^2+(-v_s)^2}=v_s\sqrt{2}\)
pa imata hitrosti enako velikost (vektorja sta enako dolga), vendar drugačno smer (na levi strani oklepa vektor s horizontalo kot
\(45^{\circ}\), na desni strani pa
\(-45^{\circ}\).