Stran 2 od 2
Re: Kompleksna analiza
Objavljeno: 27.1.2014 13:27
Napisal/-a Aniviller
blblblblbl napisal/-a:In še to..
Zapišsi holomorfno preslikavo, ki predstavlja rotacijo za kot π/4 okoli točke z = 2i v
pozitivni smeri. Kam se preslika točka i?
Ah... tako kot ponavadi. Premakni v izhodišče, zavrti okrog izhodišča in premakni nazaj:
\(e^{i\pi/4}(z-2i)+2i\)
Re: Kompleksna analiza
Objavljeno: 27.1.2014 14:20
Napisal/-a Aniviller
blblblblbl napisal/-a:Pozdravljeni!
Ponovno se mi je zataknilo pri kompleksni analizi, tokrat pri razvojih v Laurentove vrste.
Naloga je naslednja:
Razvij funkcijo f(z) = z/((z^2 − 4)(z^2 − 1)) v Laurentovo vrsto, ki konvergira na 1 < |z| < 2.
Funkcijo sem razstavila na parcialne ulomke. Zdaj pa nevem kako veš ali razviješ posamezne dele v Taylorjevo ali v Laurentovo. Vem, da je potrebno gledati konvergenčni radij ampak jaz ponavadi najprej razvijem in potem pogledam konvergenčni radij.
Upam da sem napisala dovolj razumljivo kaj mi ni jasno.
Hvala že vnaprej!
Laurentova vrsta je specifično tista, ki ima vse negativne potence centrirane v isti točki. Noben izmed polov ni direktno v sredini... pola pri +-1 preprecujeta, da bi navadna Taylorjeva vrsta konvergirala nad |z|>1. Laurentova vrsta konvergira med zgrešenimi poli negativnih delov (tistimi, ki jih negativne potence direktno ne opišejo), in med poli Taylorjevega prispevka. Torej moraš 1/(z^2-1) razvit po Laurentovi vrsti, 1/(z^2-4) pa po Taylorjevi, če hočeš dobit željeno območje konvergence.
In to: simetrija ti bo dosti pomagala, če razbiješ po parcialnih ulomkih samo do kvadratnih členov.
Re: Kompleksna analiza
Objavljeno: 12.3.2015 14:43
Napisal/-a subic.alja
Pozdravljeni,
imam težave z nalogo v priponki, če bi mogoče kdo znal priskočiti na pomoč.
LP
Re: Kompleksna analiza
Objavljeno: 13.3.2015 10:21
Napisal/-a Zajc
Izberimo \(z_0=x_0+iy_0\in U\), da je \(f'(z_0)\ne 0\). Potem je diferencial funkcije \(f:\mathbb{R}^2\to\mathbb{R}\) v točki \((x_0,y_0)\) različen od \(0\). Recimo, da je \(\frac{\partial f}{\partial y}(x_0,y_0)\ne 0\). Po izreku o implicitni preslikavi potem obstaja \(\mathcal{C}^2\) funkcija \(y=y(x)\) v okolici točke \(x_0\), tako da je \(f(x,y(x))=f(x_0,y_0)\). Torej je \(g(x,y)=f(x,y)-f(x_0,y_0)\) holomorfna funkcija, ki ima množico ničel s stekališčem in zato \(g=0\). Torej je \(f\) konstantna.
Re: Kompleksna analiza
Objavljeno: 29.5.2015 12:29
Napisal/-a subic.alja
Živjo,
ponovno imam problem z nalogo v prilogi, če bi kdo morda znal pomagati.
LP
Re: Kompleksna analiza
Objavljeno: 30.5.2015 13:30
Napisal/-a Zajc
Imenovalec razviješ v Taylorjevo vrsto in dobiš \(\frac{z^3}{3!}-\frac{z^5}{5!}\pm\ldots\). Ker se členi začnejo pri \(z^3\), gre za pol stopnje \(3\). Potem lahko še z L'Hospitalom preveriš, da ima funkcija \(f(z)z^3\) res limito v točki \(0\). Za izračun glavnega dela pa v bistvu računaš prve tri člene v razvoju funkcije \(f(z)z^3\) v Taylorjevo vrsto (najlažje kar z odvajanjem).
Re: Kompleksna analiza
Objavljeno: 2.6.2015 9:00
Napisal/-a anja8
Zdravo.
Tudi jaz se mučim z eno nalogo:
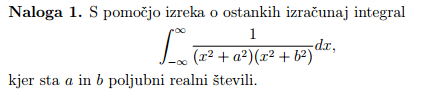
- Zajeta slika.PNG (14.08 KiB) Pogledano 4649 krat
Hvala za pomoč.

Re: Kompleksna analiza
Objavljeno: 2.6.2015 16:19
Napisal/-a Zajc
To nalogo se da sicer izračunati tudi brez kompleksnih integralov (razcep na paricalne ulomke, pridejo neki arkus tangensi ...).
Predpostavimo, da je \(a>0\) in \(b>0\) (če je kakšen enak \(0\), integral divergira). Funkcija \(f(z)=\frac{1}{(z^2+a^2)(z^2+b^2)}\) ima pole v \(z_1=ai,z_2=bi,z_3=-ai,z_4=-bi\).
Najprej predpostavimo, da je \(a\ne b\).
Naj bo \(R\) poljuben, tako da je \(R>a\) in \(R>b\). Označimo z \(\gamma_R\) pozitivno orientirano sklenjeno polkrožnico s polmerom \(R\) okrog izhodišča (t.j. \(\gamma_R=[-R,R]\cup\{Re^{it}|\ t\in[0,\pi]\}\). Znotraj te krivulje sta le pola \(z_1\) in \(z_2\). Torej je po izreku o ostankih \(\oint_{\gamma_R}f(z)dz=2\pi i(Res(f,z_1)+Res(f,z_2))\). Integral na levi razbijemo na dva integrala in dobimo \(\int_{-R}^Rf(x)dx+\int_{K_R}f(z)dz=2\pi i(Res(f,z_1)+Res(f,z_2))\), kjer je \(K_R=\{Re^{it}|\ t\in[0,\pi]\}\). Drugi kos gre proti \(0\), saj je \(|\int_{K_R}f(z)dz|\le\int_{K_R}\frac{dz}{|z^2+a^2|\cdot|z^2+b^2|}\le\int_{K_R}\frac{dz}{|\frac{z^2}{2}|\cdot|\frac{z^2}{2}|}=\int_{K_R}\frac{4dz}{R^4}=\frac{4}{R^4}\cdot(-2R)\) (upoštevali smo, da je \(|z^2+a^2|=|z^2|\cdot|1+\frac{a^2}{z^2}|\ge\frac{|z^2|}{2}\) za dovolj velike \(z\), in podobno \(|z^2+b^2|\ge\frac{|z^2|}{2}\)). Torej je \(\int_{-R}^Rf(x)dx\to 2\pi i(Res(f,z_1)+Res(f,z_2))\). Izračunamo še residuuma. Ker gre za pole stopnje 1, je \(Res(f,ai)=f(z)(z-ai)|_{z\to ai}=\frac{1}{2ai(b^2-a^2)}\) in podobno \(Res(f,bi)=\frac{1}{2bi(a^2-b^2)}\). Vstavimo in dobimo \(\int_{-\infty}^{\infty}f(x)dx=\frac{\pi}{ab(a+b)}\).
Če je \(a=b\), je postopek enak, le da gre za en sam pol stopnje 2. Residuum je v tem primeru enak \(Res(f,ai)=\frac{d}{dz}[f(z)(z-ai)^2]|_{z\to ai}=-\frac{2}{(z+ai)^3}|_{z=ai}=\frac{1}{4a^3i}\), kar pripelje do rezultata \(\int_{-\infty}^{\infty}f(x)dx=\frac{\pi}{2a^3}\).
Re: Kompleksna analiza
Objavljeno: 4.6.2015 8:36
Napisal/-a anja8
Ojej, izgleda zelo zahtevno!
Hvala Zajc, tole je bilo v veliko pomoč!
